3.1 寿命和衰老的进化理论基础

The 进化ary theories of longevity and aging have their roots firmly planted in basic concepts of 进化ary biology. In this section, we briefly explore topics in general 进化 that significantly influenced the development of 进化ary models related to longevity and aging.

 

3.1.1 Weismann established the separation between soma and germ cells

At the time of Darwin‘s death in 1882, 进化 by natural selection had not yet been fully accepted by the biological sciences community. Although most biologists of the time agreed that Darwin was undoubtedly correct, the theory still had many holes that prevented its complete acceptance. One such problem was the mechanism by which traits were passed between generations. Most scientists of Darwin‘s time believed that the soma (body) cells transmitted the properties of heredity directly to the germ (sex) cells, or gametes. It was not until the great German theorist August Weismann (1834–1914) proved otherwise that our current concept of a division between somatic cells and germ cells was established. This set the basis for a theory on aging. In one experiment, Weismann mated mice that had had their tails cut off, prior to reproductive age, for 22 generations. Each mated pair produced mice with tails(Figure 3.1). This experiment showed that body cells were not communicating with the sex cells and that gametes alone transfer the chemicals of inheritance to the next generation.

 Figure 3.1 Weismann‘s experiment establishing the separation between germ line (sex cells) and soma (body cells). Weismann discovered that removing the tails of mice before the start of reproduction had no effect on the appearance or length of tails in the offspring, generation after generation.

 

The separation between soma and germ cells suggested to Weismann a division of labor within the organism: somatic cells existed solely to support the germ cells and their function of passing on the “stuff” of inheritance. Based on this evidence, Weismann theorized that the soma‘s job was to ensure that the individual lived long enough to reproduce. Once this job was done, there was no further need for the soma, and aging and death of the organism would follow. As you will see later in this chapter, Weismann‘s thoughts on aging form the basis of what would later be called the trade-off hypothesis, which suggests that cost of successful reproduction is mortality.

3.1.2 Weismann proposed that aging is a nonadaptive trait

In Weismann‘s first writing on the subject of 进化 and aging, he states that . . . in regulating duration of life, the advantage to the species, and not to the individual, is alone of any importance. This must be obvious to anyone who has once thoroughly thought out the process of natural selection. It is of no importance to the species whether or not the individual lives longer or shorter, but it is of importance that the individual should be enabled to do its work towards the maintenance of the species. This work is reproduction or the formation of a sufficient number of new individuals to compensate the species for those which die. As soon as the individual has performed its share in this work of compensation, it ceases to be of any value to the species, it has fulfilled its duty and it may die. (Weismann 1891)

This early writing by Weismann suggested that aging arose through natural selection as a positive adaptation that worked for the good of the species, a general concept known as group selection. That is, selection occurs at the level of the group rather than the individual. Weismann originally believed that aging is selected to rid the group of old and useless individuals who are no longer capable of reproduction but continue to use limited and valuable resources, such as food and water. Ridding the group of nonreproducing adult members who do not contribute to continuation of the species allows resources to be preferentially allocated to the reproductively active members of the group, and the fitness of the remaining group increases.

Weismann’s logic of the group benefit in ridding the species of older, nonreproducing adult members has obvious appeal and remains a common misconception. Evidence from studies in molecular 进化 has conclusively established that the individual—or, more precisely, the gene—is the focus of adaptation, precisely what Darwin originally believed. Only reproductively active individuals influence the makeup of the genome, and this makeup is driven exclusively by the need of the individual to achieve reproductive age and pass on the gene. In other words, the gene does not “know” that in later years, the group would need to rid itself of old people. In fact, some evidence now exists to suggest that menopause (reproductive aging) and the extended postreproductive life span may be an adaptation that increases fitness

 

BOX 3.1  THE GRANDMOTHER HYPOTHESIS AND FEMALE LONGEVITY

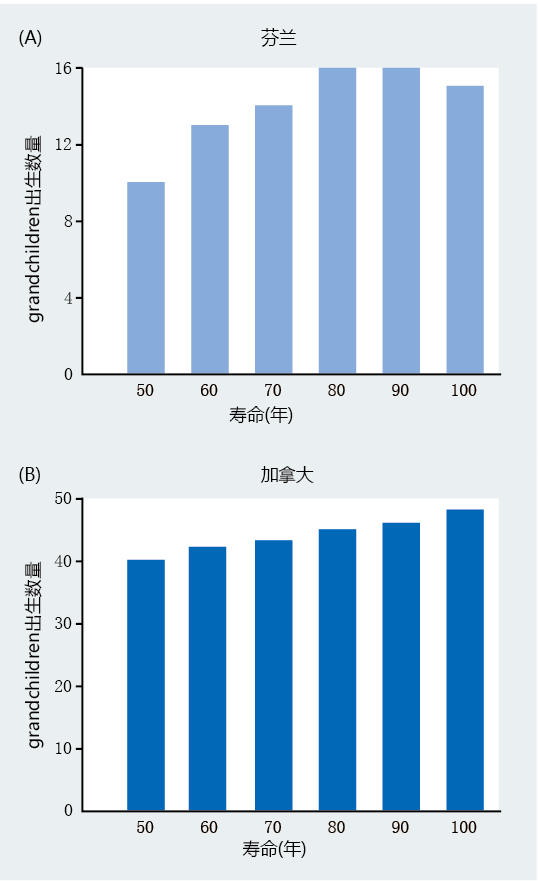
Throughout history, human grandmothers have been portrayed as kind and loving members of an extended family who provide care to their grandchildren. Many cultural anthropologists believe that the grandmother–grandchild relationship separates our species from all others, including nonhuman primates. A few anthropologists now suggest that the relationship between the grandchild and the grandmother transcends a simple emotional connection and may have had a role in the 进化ary development  of  longevity.  The grandmother hypothesis posits that care given by grandmothers to children in early societies allowed their daughters to have more children and thus increase overall fitness for the species. The longer the grandmother lived, the more children her daughter could have, and the greater the fitness. That is, longevity—or, at least, the long post-reproductive life span observed in humans—was selected because of its benefits to reproductive success.  The grandmother hypothesis is an extension of the theory of G.C. Williams that menopause might be an adaptation that increases overall fitness for the species. Williams suggested that in 进化ary history, older mothers ran a greater risk of dying during childbirth and thus would be unable to provide for their surviving children. Death of these offspring would result in decreased fitness for the species. If, however, older women were physiologically unable to reproduce because of menopause, older mothers could focus on providing resources to the offspring that already existed. Similarly, the grandmother hypothesis suggests that a long postreproductive life span evolved as a result of the grandmother’s help in rearing their daughters' older offspring. This would allow the mother to focus greater resources on the younger offspring that were still totally dependent on her. The grandmother was essential to the survival of her grandchildren. Thus, a long postreproductive life span increased fitness.  Studies evaluating demographic data collected in the eighteenth and nineteenth centuries have generally supported the grandmother hypothesis. The researchers selected several measures of fitness, including (1) mothers having more offspring; (2) mothers reproducing earlier and more often; and (3) mothers having shorter interbirth intervals. The researchers found that the number of grandchildren correlates directly with the life span of the grandmother (Figure 3.2): the greater the age of the grandmother, the more grandchildren. Investigators also found that their measures of fitness were enhanced when the grandmother lived in the same house as her daughter and provided care for the grandchildren, compared with families that did not include the grandmother. Based on these findings, the authors concluded that “our results lend strong support for the hypothesis that prolonged female postreproductive lifespan is adaptive, to our knowledge revealing for the first time the substantial fitness benefits that females accrue by living beyond reproductive age.” Figure 3.2 Relationship between female lifespan and total number of grandchildren contributed to the following generation.  Data are shown (A) for Finland (1702–1823) and (B) for Canada (1850 –1879). The rise in slope for each population is the equivalent of postreproductive women gaining two extra grandchildren for every 10 years the women survived beyond age 50. (From M. Lahdenpera et al., Nature 428:178–181, 2004. With permission from Nature Publishing Group.)   Other studies have not found a “grandmother benefit” for species fitness, but have demonstrated that inclusion of the grandmother as a caregiver for her daughter‘s children shortened the interbirth interval. If a grandmother was able to care for recently born children, the mother could reproduce quickly and have more children than a woman without grandmother care. More children means greater fitness, and the short interbirth interval would sooner or later be dominant in the population. The grandmother hypothesis can be very appealing and does have scientific  credibility.  Nonetheless, there are some questions that need to be answered before this hypothesis receives widespread acceptance. First, were there enough women having long postreproductive life spans throughout our 进化ary history to increase fitness? Recall from Chapter 2 that the average life span throughout most of history has hovered around 35–40 years of age and that less than 2% of the population lived beyond 60 years of age. Children born into families without grandmothers would have vastly outnumbered children in families having grandmothers. Thus, selection pressure—the events altering the genetic composition of individuals (in this case, a grandmother providing care)—for a gene giving rise to a long postreproductive life span or enhanced longevity may not have been strong enough to influence gene selection. Second, is it possible that older male and female siblings contributed to the care of dependent children? If, for example, the care was provided primarily by an older sibling, the selection pressure for a longevity gene would not just be weak, it would be nonexistent. Given the scarcity of old people in prehistoric populations, it seems more likely that care of dependent children would fall to an older sibling rather than a grandmother. At the very least, there would have been considerable variation in who cared for the dependent child.  Finally, what were the family structure and responsibilities? The overwhelming majority of early societies were patriarchal. It was the male, not the female, who provided the most important care—the gathering of food—for the dependent child. The grandmother may have provided emotional, nursing, and palliative care for dependent children, an important job to be sure, but insignificant compared with the biological necessity of food. Without the male providing food for the family, there wouldn‘t have been a grandmother on which to base a hypothesis. There is little doubt that grandmothers have played an important role in the care of grandchildren throughout history. It is even possible that grandmothers contributed more to child rearing during 进化ary history, allowing their daughters to have a greater number of children. Whether the greater number of children increased species fitness and resulted in the adaptive trait of a long postreproductive life span remains to be seen. The data supporting the grandmother hypothesis are neither extensive nor compelling and rely almost exclusively on correlative rather than causal analysis. However, we should not dismiss out of hand any hypothesis for which at least some supportive research exists. With supportive mathematical models and highly controlled laboratory research, we may just find that grandma has been more important to the family than just being able to prepare a great dinner.

 

In time, Weismann became aware that his original view on group selection as the basis for his theory of aging conflicted with Darwin's proposal that natural selection works on the variation among individuals within a species. Weismann had to either reject Darwin's natural selection theory or revise his own view on the 进化ary basis of aging. He chose the latter. Weismann formulated his new theory based on the thought that as soon as a trait becomes useless to an individual, natural selection no longer acts to either remove or maintain the trait. Recall that Weismann saw the post-reproductive period as having no value to the organism. Since most of the physical problems of aging occur after reproduction, the traits of aging neither increase nor decrease fitness, so aging and/or senescence are neutral to the forces of natural selection. Weismann referred to such traits as nonadaptive traits. The neutrality of aging allowed Weismann to retain his suggestion that a postreproductive period in multicellular organisms is useless, while at the same time maintaining his strict Darwinist view.

The appearance of neutral or nonadaptive traits has often caused confusion when seen in the light of Darwin‘s ideas of variation, fitness, and adaptation. This confusion undoubtedly arises as a result of the exclusive focus on natural selection as the only force of 进化. But even Darwin recognized that traits could become “fixed” without the force of natural selection:

Variations neither useful nor injurious [to reproduction] would not be affected by natural selection, and would be left either a fluctuation element, as perhaps we see in certain polymorphic species, or would ultimately become fixed... (Darwin, 1859)

Thus, aging could have arisen without an influence on reproduction. As you’ll see, Weismann’s thoughts on nonadaptive aging set the basis for theories that predict that the neutral trait of aging is either a by-product of genes fixed for a reproductive advantage or a random expression of genes in older age groups.

3.1.3 Population biologists developed logistic equations to calculate population growth

Mendel’s principles of inheritance were not introduced formally into 进化ary theory until the early 1900s. Therefore, neither Darwin nor Weismann was able to incorporate Mendel’s findings into their theories. Mendel provided the answer to the question of how variation, underlying Darwin’s fundamental principle of natural selection, arose in a species. According to Mendel, variation occurred because the alleles for (that is, different versions of) a specific gene transmitted by each parent to the offspring can have slightly different forms. The question then became, “At what rate and by what mechanisms do these alleles become dominant in a population?” Research into such questions gave rise to a new form of 进化ary analysis, population genetics, a science that focuses on the origin of allele variation in a population.

进化ary theories of aging and longevity rely on some basic principles of population genetics to better explain how life span in a population is affected by the frequency at which an allele that enhances reproduction appears in a species’ genome. Determining the rate at which an allele appears in a population requires a basic understanding of reproductive potential—a species' relative capacity to reproduce itself under optimal conditions—and the population's growth.

Unicellular (single-cell) species, such as Saccharomyces cerevisiae; simple multicellular organisms, such as Caenorhabditis elegans; and cells from multicellular species grown in cultures—all are being used to understand the basic mechanisms underlying aging and longevity. Although S. cerevisiae, C. elegans, and cells growing in culture propagate by different mechanisms, they have similar patterns of growth. These growth patterns have a significant effect on the population's life span.

The rate of growth in populations of simple organisms reflects the birth rate minus the death rate and is called the intrinsic rate of natural increase, r. However, reproduction and growth in all species, simple and complex, are constrained by 环境al factors such as food, space, and temperature that significantly influence the population's growth and reproduction potential. These and other constraints are collectively known as the carrying capacity of a population, K, or the constraints placed on population size due to 环境al factors. These concepts are used in the Verhulst-Pearl logistic equation (Equation 3.1) to describe population growth for any population, particularly populations that are constrained by lack of mobility and/or are maintained under highly controlled conditions. Verhulst-Pearl logistic equation:

where

N = population size

r = intrinsic rate of natural increase

K = carrying capacity of the population

 

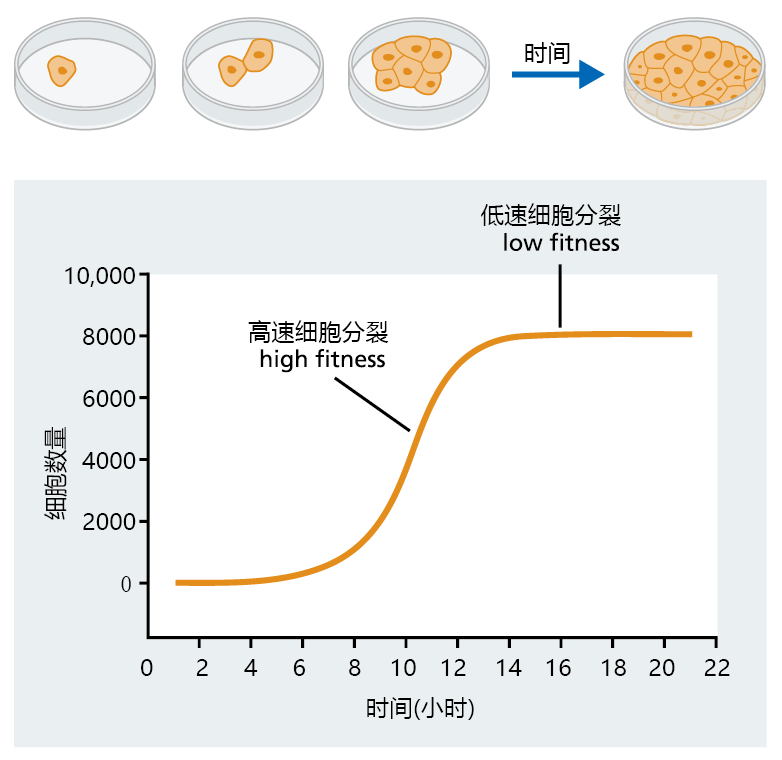
Figure 3.3 illustrates how constraints on simple organisms can affect growth and reproduction and influence gene selection. Growth in the cell population during the initial stages of culture is slow, due to a small population of “parent cells.” As the population of cells increases, so does the growth rate, since there are more “parent cells” to produce offspring. Growth of the population during this period is driven almost exclusively by the intrinsic rate of natural increase, since food is abundant and space is plentiful. As food supply and space begin to shrink, the rate of reproduction slows, as does the population growth. Finally, the space and food necessary to support the size of the population run out. If more food and space are not provided, the population of cells will senesce and die. The logistic equation of population growth becomes important when we discuss replicative senescence in Chapter 4.

 

 

Figure 3.3 Population growth in a hypothetical cell population, as described by the Verhulst-Pearl logistic equation.  In this cell population, the constraint on population growth is represented by space (size of the container) and food. Note that the period of high fitness occurs early in the life span of the culture, when cell division is greatest. Low fitness occurs late in the life span, when population growth slows and plateaus.

 

This simple example demonstrates a fundamental principle of population genetics that has great importance to the 进化 of aging and longevity: The age at which high rates of reproduction occur have the highest level of Darwinian fitness, due simply to the number of individuals that are reproducing. As reproduction slows, fitness declines. Thus, alleles that convey traits important to survival and reproduction are selected over alleles that impart longevity. This important concept helped population geneticists formulate theories of how genes selected for survival also determine the length of life.

3.1.4 A population's age structure describes Darwinian fitness in complex eukaryotes

More advanced eukaryotes are not constrained by 环境 conditions to the same degree as described in our previous example. The mobility of complex eukaryotes allows animals to search for food and water, find shade on hot days, and move to insulated locations on cold days. Therefore, for complex eukaryotes, mobility means that 环境 constraints, or K factors, are variable. Determining the rate at which alleles are fixed in complex eukaryotes that have variable K factors requires a more complex set of equations than the logistic equations used for simple organisms. These equations describe a population's reproductive contribution to future generations, or species fitness, at any given time during the life span and constitute a method known as age-structure analysis.

Age-structure analysis can be used to determine whether a particular age group within a population contributes to the action of natural selection on that population. It can also be used to answer the question, “At what age is an individual most likely to pass on traits beneficial to the species’ survival?” Knowing when specific alleles are most likely to be selected provides information on whether aging, senescence, and/or longevity arose through natural selection.

In Chapter 2 you were introduced to the concept of age-structure analysis in the calculation of survival (l x ), using variables in the life table. As a component of fitness, survival predicts how many individuals are available for reproduction in a specific age group. Because survival declines with each successive age group after the onset of reproduction, it would seem that fitness might also decline. However, survival provides only a marker of potential fitness. To calculate actual fitness in a population, we need to include a measure of the reproduction rates. This measure is known as fecundity, m x .

For age–structure analysis, the population is stratified into age groups. The process of age grouping has no set standard but primarily reflects the reproductive characteristics of the population. Periodic-breeding populations, such as animals that breed only once per season (most birds and reptiles), are typically grouped by the number of breeding seasons. Populations in which reproduction occurs continuously (most mammals) are generally grouped by a convenient time interval, in days, months, or years.

3.1.5 Reproduction rate describes age-specific fitness in breeding populations

Age-structure analysis in periodic-breeding populations is simplified by the fact that offspring are produced at regular intervals—in the breeding season. Algebraic equations can be used to calculate both the total population and the breeding season–specific reproduction rate. The numerical results of these equations are referred to as the net reproduction rate  (Equation 3.2) . The net reproduction rate for a population (R 0 ) is the sum of all breeding season–specific survival rates (l x ) multiplied by breeding-specific fecundity (m x ).

Net reproduction rate,

 

where

R 0 = potential number of offspring produced by a newborn over its life span

l x = survivorship, calculated from a life table

m x = fecundity

The net reproduction rate provides a measure of reproductive power and, thus, fitness. It is most often used in analysis of periodic-breeding populations. When the net reproduction rate is applied to animals with breeding seasons, it is referred to as the breeding season–specific reproduction rate and indicates which groups have the most influence on growth and fitness. For example, consider the hypothetical seasonalbreeding population shown in Figure 3.4. Predation and 环境 hardships cause survivorship to decline in each successive breeding season. However, different rates of sexual development of individuals within the population cause fecundity to increase during the first few breeding seasons. The increase in fecundity early in the population's life history will outpace the decrease in survivorship. The inverse relationship between survivorship and fecundity during the first few breeding seasons results in an increase in the breeding season–specific reproduction rate. As survivorship, fecundity, and reproduction rate decline during each successive breeding season, the population is eventually left with a small group of long-lived individuals that do not reproduce. Once again, natural selection favors alleles that enhance survival to reproductive age rather than traits that add to the length of life of the species.

Figure 3.4 Age–structure analysis using the net reproduction rate in a hypothetical, seasonal-breeding population at equilibrium ( R 0 = 1). The shaded blocks represent population size. The highest breeding season–specific reproduction rate is 0.5, in breeding season 3, reflecting an increase in fecundity. The lowest breeding season–specific reproduction rate is 0, in the youngest (breeding season 1) and longest-lived (breeding season 6) animals. That is, fitness is greatest in the younger population and lowest in the older population.

 

Equations describing populations of species that continuously reproduce require integration to determine the rate of growth. The equation describing population growth in continuously breeding populations was proposed by the statistician Alfred Lotka, who built on the work of the eighteenth-century Swiss mathematician Leonhard Euler. Thus, the equation bears both their names (Equation 3.3). Note that Equation 3.3 is simply the integration of Equation 3.2 and thus imparts the same basic information on reproductive potential and fitness. General form of Euler-Lotka equation of population growth:

 

where

e = the mathematical constant

r = intrinsic rate of population growth at time t

l( x ) = survivorship at time x

m( x ) = fecundity at time x

 

3.1.6 Fisher described the relationship between reproductive potential and Darwinian fitness in populations

The Euler-Lotka equation set the basis for R. A. Fisher’s development of a mathematical model that could be applied to theories of the evolution of aging and longevity. Fisher (1890–1962) was the first to suggest that solving for r, the intrinsic rate of natural increase, in Equation 3.3 provides a measure of fitness for an individual in a population. Since Fisher‘s primary interest was predictive statistical analysis, he was more concerned with how the current population growth could predict future individual fecundity and fitness. To this end, Fisher derived a measure, the reproductive value, v x , which he suggested predicted an individual‘s future reproductive contributions relative to the reproductive output of the total population  (Equation 3.4)

 

Reproductive value, v x =

where

v x = reproductive value of an individual at time x

e = the mathematical constant

r = intrinsic rate of population growth

l x = survivorship

l(t) = remaining total survivorship of the population at time t

m(t) = remaining fecundity of the population at time t

 

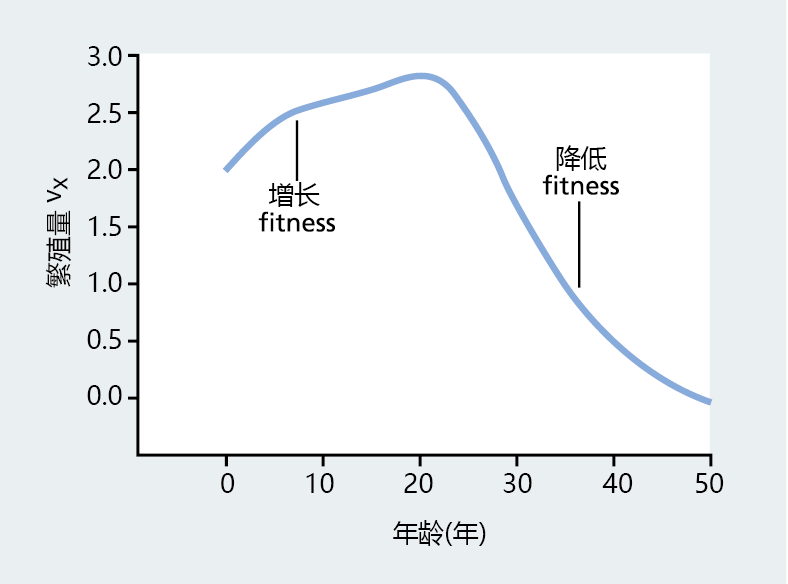
For Fisher, v x provided insight into answering the question, “At what age will an individual in a continuously breeding population have the greatest fitness?” As shown in  Figure 3.5 , the reproductive value provides a measure of potential fitness by estimating the future reproductive contribution of a specific age group.

 

Figure 3.5 Reproductive value ( v x ) of females in the Commonwealth of Australia in 1911. This graph was created by inserting recorded birth and death rates in Equation 3.4. As expected, the reproductive value is highest at young ages and decreases as the population ages, approaching the end of the reproductive life span. Note that an increase in v x indicates an increase in fitness, and a decrease in v x corresponds to a decrease in fitness. (Adapted from R.A. Fisher, The Genetical Theory of Natural Selection, Oxford: Clarendon Press, 1930.)

 

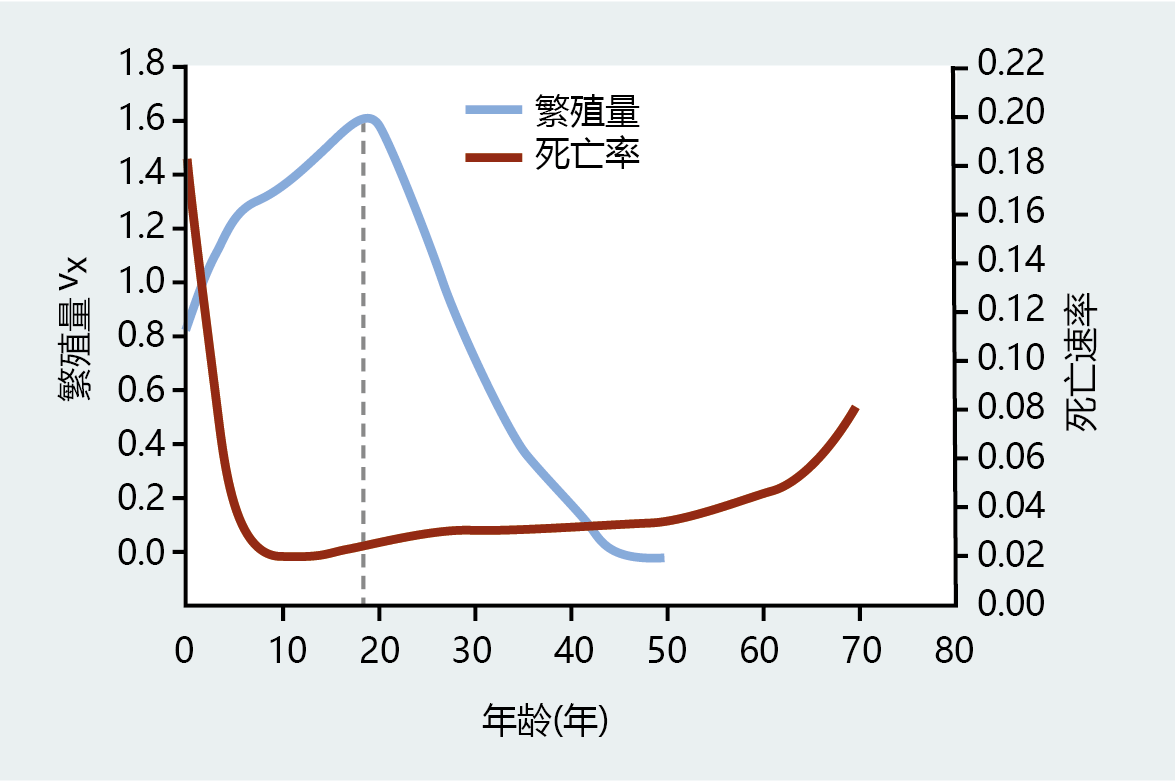
Although Fisher helped to establish the foundations for 进化 models of longevity and aging, his only allusion to a relationship between reproductive value and aging came from his observation that v x declines at about the same time that mortality begins to increase (Figure 3.6) . He suggested, for the first time, that longevity might be a by-product of alleles fixed for survival to reproductive age. A more formal application of Fisher‘s age–structure analysis to the 进化 of longevity would have to wait until the verbal postulation of Sir Peter Medawar and the mathematics of W.D. Hamilton, as described below.

 

 Figure 3.6 Reproductive value and mortality rate of Taiwanese females in 1906. Note that the mortality rate begins to increase at roughly the same time that reproductive value, v x , begins to decrease, at the point indicated by the dashed line. (Adapted from R.A. Fisher, The Genetical Theory of Natural Selection, Oxford: Clarendon Press, 1930.)