3.2 进化和寿命

3.2.1 The extrinsic rate of aging leads to a decline in the force of natural selection

The first serious application of Weismann's and Fisher's hypotheses on longevity came from Sir Peter Medawar (1915–1987). Medawar used a simplified version of age–structure analysis to establish that the life span of all matter, inorganic and organic, results from extrinsic factors. Moreover, demonstration of the extrinsic rate of aging—the rate of aging in a population due to 环境al hazard—established what many believe to be the fundamental principle underlying the 进化ary basis of longevity: the force of natural selection declines with age.

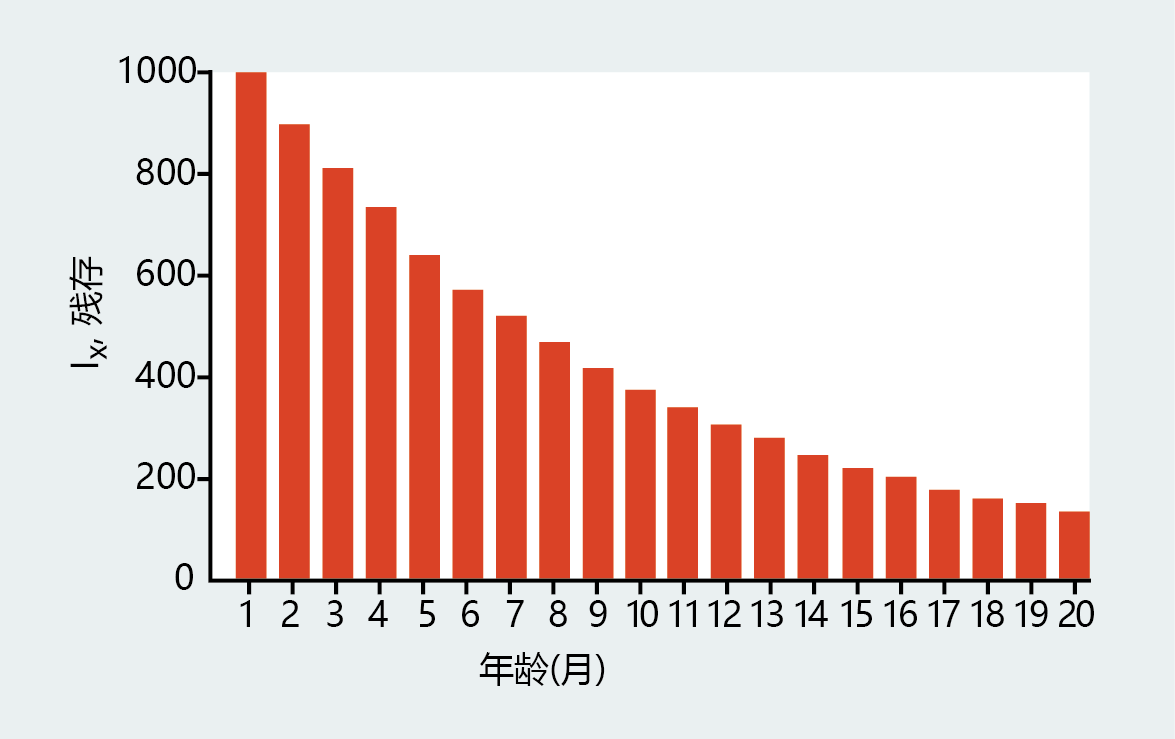
In 1951, Medawar proposed a thought experiment that demonstrates this principle. Imagine a start-up laboratory that has a “population” of 1000 test tubes. Although the test tubes do not age, each month, exactly 10% of the test tubes are broken in random accidents—extrinsic, 环境al factors. Personnel in the laboratory replace the broken tubes so that the total population is always 1000 at the beginning of each month. That is, the total population of test tubes is at equilibrium. Fortunately for our demonstration, the director of the laboratory requires that all test tubes be marked with the date they entered the population. Thus, we can follow the life history of the original population of 1000, as shown in Figure 3.7 .

Figure 3.7 Life history of a test tube “population” in Medawar's thought experiment. This graph shows the number of surviving test tubes (survivorship, l x ) from an original immortal population of 1000, assuming a fixed probability of death of 10% per month. (Adapted from P.B. Medawar, An Unsolved Problem of Biology, London: H.K. Lewis & Company, 1952.)

The age-structure distribution illustrated in Figure 3.7 describes a population in which the survivors of any age group always outnumber the survivors in the subsequent age group. In this population, greater survivorship of the test tubes of one group compared with the next group cannot be due to increased fragility, because there is no aging—that is, no intrinsic factor that increases the probability of death. Death occurs simply because, with increasing age, the test tubes are exposed for a longer time to extrinsic hazards of the 环境 and thus have an increased risk of being broken. Through this description of a non-enescing, extremely long-lived population, Medawar established the extrinsic rate of aging. In the next chapter, you will see that the simple passage of time, with increasing exposure to the extrinsic hazards of one’s 环境, forms the very basis for the physiological decline associated with aging.

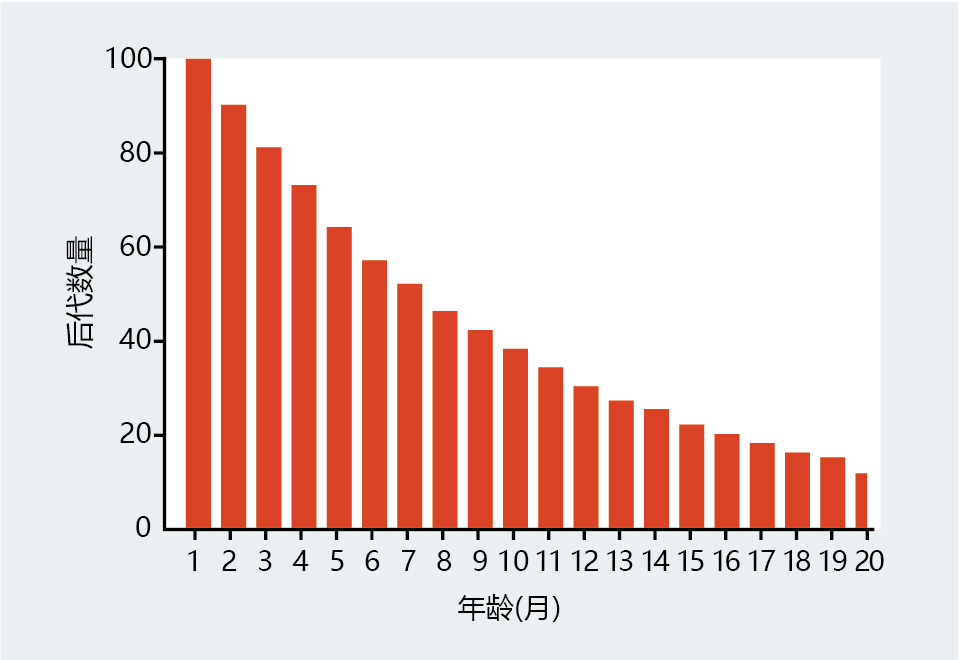
We'll now change the parameters a little. Instead of having the laboratory personnel replace the test tubes, we assume that each age group in the population described in Figure 3.7 has been, miraculously, given the ability to reproduce. As luck would have it, they reproduce at a constant rate of 10% per month (Figure 3.8). The tubes still do not age, and all individuals, no matter how old, have equal fertility. However, that does not mean that each age group will contribute equally to the renewal of the total population. Clearly, the number of test tubes in the 1–2 months age group (10% of 900) is much larger than the number of test tubes in the 13–14 months age group (10% of 273). Thus, younger populations make a greater contribution to the replacement of the population, not because they are more virile, but simply because they have not been exposed to 环境al hazards as long as the older populations.

Figure 3.8 Relationship between number of offspring and age of Medawar's test tube “population.” Assuming that the test tubes reproduce at a constant rate of 10% per month and that the probability of death remains fixed at 10%, younger populations will produce more offspring than the older groups, because there are more younger test tubes than older test tubes. This simple observation by Medawar describes the reason for the decline in the force of natural selection with age. (Adapted from P.B. Medawar, An Unsolved Problem of Biology, London: H.K. Lewis & Company, 1952.)

In the next step of this demonstration, the test tubes are no longer intrinsically immune to aging. At some age they become feeble and lose the ability for self-reproduction. Does the age at which reproduction begins to wane matter to the survival of our test tube population? It most certainly does. Imagine that the loss of reproduction occurs early in the life span, say, at 2–3 months of age. The consequences will be catastrophic to the continuation of the species and the test tubes will soon be gone from our laboratory. If, however, senescence and loss of reproduction occur at 15–16 months, the results will clearly decrease the total number of offspring but will not have a significant impact on continuation of the species. In other words, whether or not the older age group contributes to the gene pool of test tubes becomes irrelevant. The force of natural selection declines as fitness approaches zero.

3.2.2 Medawar theorized that aging arose as a result of genetic drift

Medawar‘s explanation for the 进化ary process by which aging and/or longevity became fixed in the organism had the same paradox that troubled Weismann. That is, if the force of natural section declines with age, and aging occurs after the start of reproduction, then how did the physiological declines associated with aging become part of the organism‘s genetic makeup? Recall that Weismann solved the paradox by suggesting that aging was neutral with respect to reproduction. Because Weismann‘s thoughts were developed before Mendel‘s principles of inheritance were known, he could not explain his reasoning in terms of classical genetics. Medawar, on the other hand, lived at a time when the principles of inheritance had been firmly established and most scientists believed in genetic determinism, the process in which genes were selected only by natural section and only for a specific biological process. (We now know that there are other mechanisms for gene selection and that one gene can be involved in several related but separate processes.) Thus, Medawar needed a theory that could explain how aging, a process contrary to survival and reproduction, could arise and be regulated by genes in the absence of natural selection. He based his explanation for the appearance of aging on the principle of genetic drift, a process in which genes can be fixed in a small population as a result of the random sorting of alleles at the time of meiosis. Medawar‘s theory on the 进化 of aging has come to be known as the mutation accumulation theory of senescence.

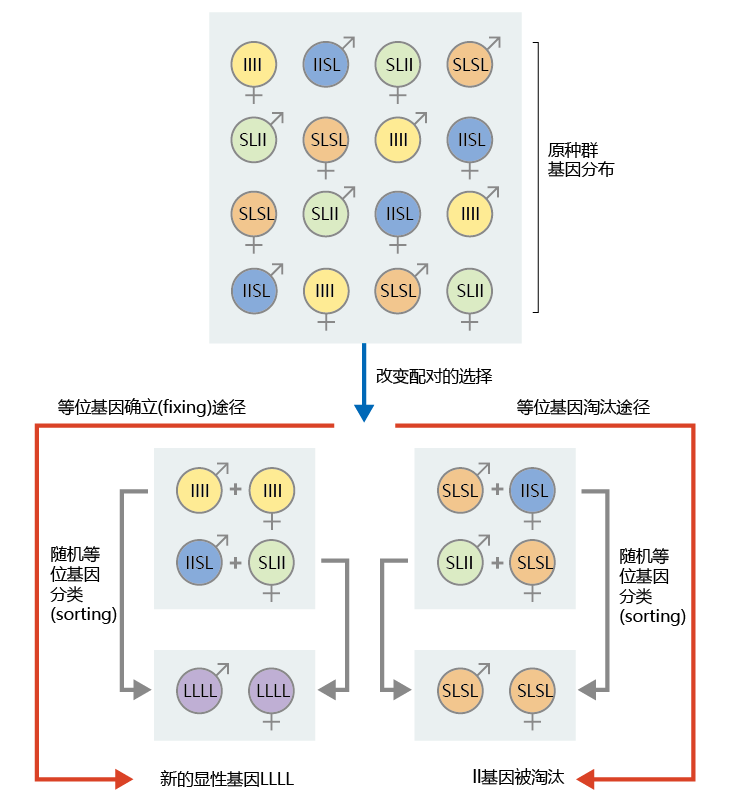
Let's look at an example. Say that a small, older population has two alleles of a gene that codes for a post-reproductive life span: a dominant allele causing short post-reproductive life span (SL) and a recessive allele causing a longer post-reproductive lifespan (ll). As shown in Figure 3.9 , this small, senescent population separates genetically into a classical Mendelian distribution: ¼ recessive and ¾ dominant (¼ llll, ½ SLll, ¼ SLSL). Because of the high extrinsic rate of aging and low fitness of the older population, only two mating pairs (four individuals) are capable of reproduction. These mating pairs arise purely by chance. In a path leading to fixing of the ll allele (left path in Figure 3.9), both individuals of one mating pair contain two copies of the recessive allele; both individuals of the other pair contain one copy each of the ll and SL alleles. For the completely recessive mating pair (llll), the only possible offspring are also completely recessive. It is also possible that the mating pair with mixed alleles produces an offspring that is completely recessive, through random sorting of alleles at the time of meiosis. Thus, purely by chance, but nonetheless a real possibility, the recessive ll allele becomes the dominant gene LLLL. A similar statistical strategy can be demonstrated for elimination of the ll allele (shown in the right path in Figure 3.9).

Figure 3.9 Gene fixing due to genetic drift and mutation accumulation. In this population, SL is a dominant allele causing short postreproductive life span and ll is a recessive allele causing long postreproductive life span. The left path illustrates how chance mating and random sorting of alleles can cause the recessive ll allele to become the dominant gene LLLL. The right path illustrates how the recessive ll allele can be eliminated from the population.

3.2.3 Medawar proposed that aging and 寿命 arise separately in postreproductive populations

Recall that Medawar lived in a time when genetic determinism was completely accepted. If a biological event was observed—and aging was viewed as a biological event—then there was a gene regulating that process. Therefore, Medawar needed to explain in genetic terms how senescence, the slow decline in function during the post-reproductive period, was regulated. He reasoned that a single gene could not cause senescence, as a single gene with massive deleterious effects would eventually be eliminated from the genome. Rather, senescence more closely reflected the fixation of hundreds if not thousands of genes that had small, non-lethal, but negative effects. Medawar's thoughts on the 进化ary basis of aging arose from the example of the disease Huntington's chorea. Huntington's chorea is a neurological disorder resulting from a recessive mutation that is expressed at midlife (late thirties to mid-forties) and is always fatal. Thus, if a single gene were responsible for aging, those carrying the Huntington‘s chorea gene would have been eliminated from the population before genetic drift could fix the gene in the genome. On the other hand, non-lethal, deleterious genes could become fixed (1) because selection pressure against these genes would be low, due to the small population involved in passing on the gene, and (2) because of genetic drift.

Medawar’s writing does not make clear whether he understood that extrinsic factors leading to the breakdown of molecular structures could result in the aging of organic life. Most likely, and in keeping with the science of his era, Medawar would have thought that organic matter would not be subject to the same physical forces that caused non-organic matter to senesce. We now know that thermodynamic forces, including entropy, also apply to organic matter (see Chapter 4). However, Medawar established the foundations for the theory that aging arises as a stochastic process resulting from thermodynamic forces, whereas longevity evolved through natural selection as a byproduct of genes important to survival to reproductive age.

3.2.4 Hamilton's force of natural selection on mortality refined Medawar's theory

The foundation of mutation accumulation lies in the observation that a trade-off exists between fecundity and mortality; highest fecundity, and therefore fitness, occurs at a time of lowest mortality. In suggesting the possibility of mutation accumulation, Medawar relied on Fisher's parameter, r, and its derivative, the reproductive value, v x , as a measure of fitness. Medawar did not, however, explain his theory in mathematically explicit terms, a critical step in theoretical 进化ary biology. This next step in the scientific explanation of the 进化 of longevity would be taken by W.D. Hamilton (1936–2000).

Hamilton recognized that integrating reproductive potential across the entire life span was an imprecise method for measuring fitness. He hypothesized that any population, even a stable population, can fluctuate in size at different ages, depending on age-specific mortality. Fitness was more likely to reflect reproductive potential at specific ages than the total integrative value over the life span, as suggested by Fisher's reproductive value.

To quantify the force of natural selection, Hamilton derived expressions for the change in fitness with respect to age-specific mortality. Like Fisher‘s reproductive value, v x , Hamilton‘s force of natural selection on mortality, s x , declines after the start of reproduction  (Figure 3.10A) . However, unlike v x , s x is stable and highest before reproduction. Because extrinsic factors make the force of natural selection on mortality highest prior to reproduction, 进化 would have selected genes that were necessary for surviving to reproductive age. Hamilton's method for assessing aging and longevity agreed with previous work indicating that selection pressure would be extremely weak for genes that regulated aging or longevity. Therefore, if genes existed for longevity and/or aging, they must be related to genes selected for survival to reproductive age.

Figure 3.10 Hamiltion's force of natural selection on mortality and fecundity. (A) The force of natural selection on mortality, s x , acts on a hypothetical human population. Note that mortality (brown line) is highest before the start of reproduction (indicated by the dashed line). (B) A small subset of the same human population has genes coding for late-life reproduction. Since reproduction in this subset population starts later than that observed in the total population, the force of natural selection on mortality is delayed. (Adapted from W.D. Hamilton, J. Theoret. Biol. 12:12–45, 1966. With permission from Elsevier.)

Hamilton‘s mathematical theory on longevity was a monumental breakthrough in understanding how life span, not aging, evolved. Imagine, for instance, that some individuals within a small population had genes coding for late-life reproduction (Figure 3.10B). The force of natural selection on mortality would start later in the life span. From a theoretical standpoint, if there is no reproduction, there cannot be a trade-off between fecundity and mortality. For any given age throughout reproduction, this small group would have greater fecundity at older ages. Over 进化ary time, and because of genetic drift, genes that impart a long life span could be fixed within the genome. Hamilton provided the mathematical theory to suggest that longevity could have evolved.