2.2 测量人群的生物衰老
在本节中,我们将讨论人群老龄化的测量。我们的讨论将主要集中在如何测量死亡率,并将其用于评估人群的寿命和老龄化率。我们还简要介绍了精确医学的兴起及其对个人的关注将如何改变我们衡量人群老龄化的方式。人群老龄化的结果为负责制定公共卫生政策的个人和机构提供了重要信息。例如,使用确定人群老龄化方法的研究人员预测,当前儿童肥胖流行将导致成年期2型糖尿病病例显著增加,寿命缩短。这一信息促使公共卫生官员制定了旨在减少儿童肥胖症的计划,这些计划似乎奏效了。
在最后一节中讨论的个体化医学的发展可能会对确定人口老龄化率的相关性提出疑问。有人可能会问,“既然预防和治疗很快将针对个人,那么衡量人口老龄化的目的是什么?”本文的立场是,衡量人口老龄化现在比以往任何时候都更加重要。如果我们不深入了解个体化生物衰老是如何影响人口死亡率和时间依赖性功能丧失的,我们就不知道花在精确医学上的数百万美元是否兑现了其改善所有人群健康老龄化持续时间的承诺。研究人口老龄化的方法将一如既往地评估医疗干预对公众健康的有效性。
通过死亡率估计人口中的死亡人数
确定大体死亡率是相当简单的,总人口死亡率不用考虑年龄,只要有人口规模和死亡人数的准确计数即可(方程式2.1):
死亡率,M=D/P(2.1)
此处
D=人口中的死亡人数
P=人口规模
该死亡率M通常转换为标准测量值,例如每年每1000或100000人的死亡率,以便于解释和比较。
在大多数国家,测量人口中的死亡人数没有什么问题,因为法律要求对死亡进行正式记录。然而,任何特定时间的人口规模只能使用最新人口普查的数据进行估计。在美国,每10年进行一次人口普查。为了减少与估计人口实际规模相关的误差,通过使用适用于假设人口规模(如100000)的实际死亡率,将人类死亡率计算为统计概率。虽然人类死亡率被认为是估计数,但已证明它们非常精确,应被视为人口死亡率的准确描述。
也可以确定非人类种群的死亡率。在实验室条件下监测的短命物种的种群规模和死亡数量可以非常精确,因此,死亡率也是如此。然而,在长寿的野生种群中,种群数量和死亡率很难衡量。想象一下,试图计算生活在美国的特定蝙蝠物种(蝙蝠可以活20年)的种群数量和死亡数量是一项不可能完成的任务。因此,野生动物学家通常将他们的工作局限于居住高密度的小区域,比如2-3英亩,然后将死亡率外推到一般种群。
生命表包含关于死亡率、预期寿命和死亡概率的信息
生命表描述了特定年龄或年龄间隔人群的死亡特征。生命表有两种类型。队列生命表遵循在整个生命周期中可以观察到的单个出生队列种群的死亡特征。队列生命表对于寿命较短的物种或具有准确出生和死亡记录的历史种群非常有用。但是对长寿物种(包括人类)在整个实际寿命内进行研究是不现实的。在这些情况下,使用当前或周期生命表。当前生命表将活的群体的当前死亡特征应用于假设的出生队列,通常为100000(表2.2)。然后,根据在单个时间点收集的数据,使用这些值预测实际人口寿命期间的死亡率统计数据。无论是队列还是当前生命表,构建生命表中给定值的机制都是相同的。生命表可以是完整的,也可以是简略的。完整寿命表定义为寿命间隔为1年的寿命表。使用所有其他年龄组定义了一个简略寿命表,如表2.2所示的寿命表。
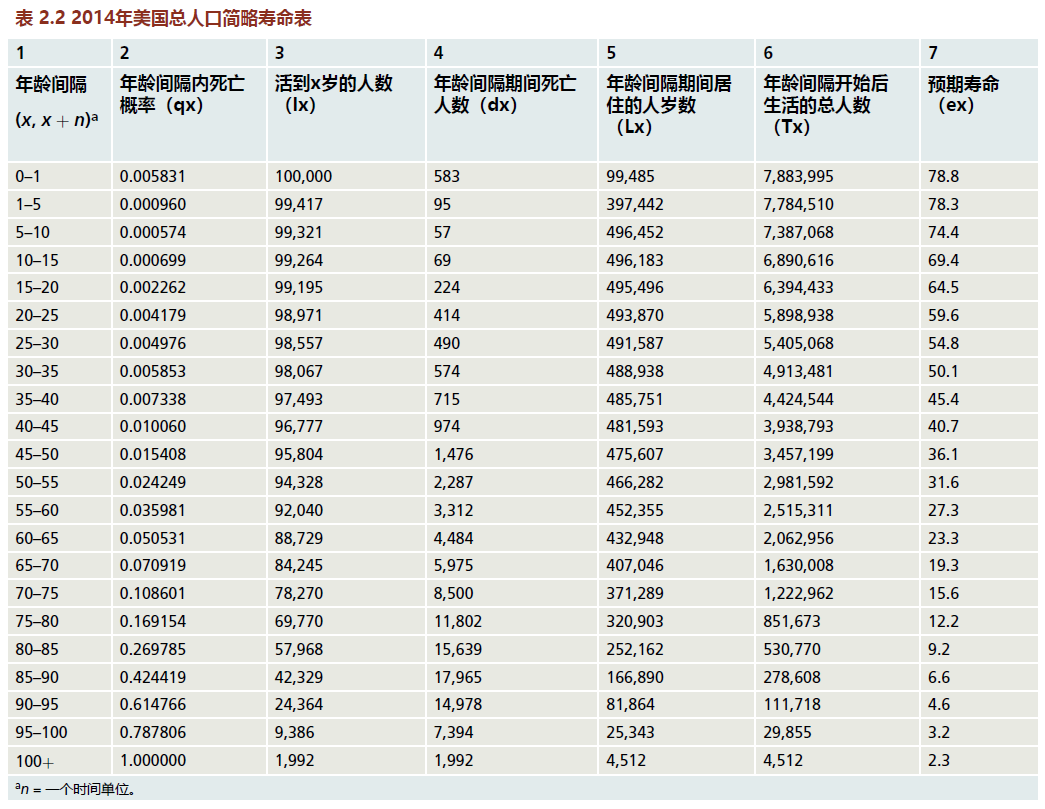
寿命表由七列组成。由于全世界都在使用寿命表作为估计人口死亡率的主要方式,因此按照惯例,列名和变量名称是标准化的。第1列包含年龄(对于完整寿命表)或年龄间隔(对于简略寿命表)。除了人类寿命表中的第一个年龄间隔(必须使用0-1年的间隔)外,年龄或年龄间隔的选择由编制该表的统计学家自行决定;对于人类数据,通常使用5年的时间间隔制作一份简略表格。第2列包含死亡概率(qx),也称为特定年龄死亡率。第3列显示了假设队列中最初10万人在年龄间隔(lx)开始时仍然活着的人数。第4列显示了每个间隔的数字(dx)。第5列“人-年寿命(Lx)”表示每个年龄段的人口在两个生日之间的总寿命(以年为单位)。第6列包含在年龄间隔x到x+n开始后的人-年总数(Tx)。最后,第7列给出了预期寿命(ex)。预期寿命是那些活到这个年龄的人的平均剩余寿命。
寿命表中包含的信息是人口统计学家的主要工具,对训练有素的专家有许多用途,这些用途远远超出了本文的范围。在这里,我们主要关注死亡率,主要是qx,以及死亡率计算得出的曲线形状如何帮助描述人口老龄化。附录1对寿命表的构造进行了更详细的描述,包括更精确的定义和计算每个变量的方法。
特定年龄死亡率呈指数增长
特定年龄死亡率(qx)是衰老研究中一个有用的衡量指标(方程式2.2)。其计算如下:
年龄别死亡率,q=dx/lx (2.2)
此处
dx=特定时间段内人群中的死亡人数
lx=活到x岁的人数
x=年龄或年龄间隔
特定年龄死亡率只是描述在特定年龄范围内死亡的机会(概率)。例如,表2.2显示了40-44岁年龄段的qx值为0.011。这意味着在这个年龄段有1.1%的死亡几率。通过绘制特定年龄段的死亡率图,我们可以直观地看到一生中的死亡率。如图2.11所示,死亡概率在成年期间缓慢增加,然后在老年期间以明显恒定的速度增加,直到整个人口死亡。特定年龄死亡率图像的形状显示出一个指数函数。Benjamin Gompertz在1825年指出了这一点,并提出,在有大量个体存活到生殖年龄的人群中,特定年龄死亡率会加快。因此,描述人口死亡率的函数以他的名字命名:Gompertz死亡率函数(方程式2.3): 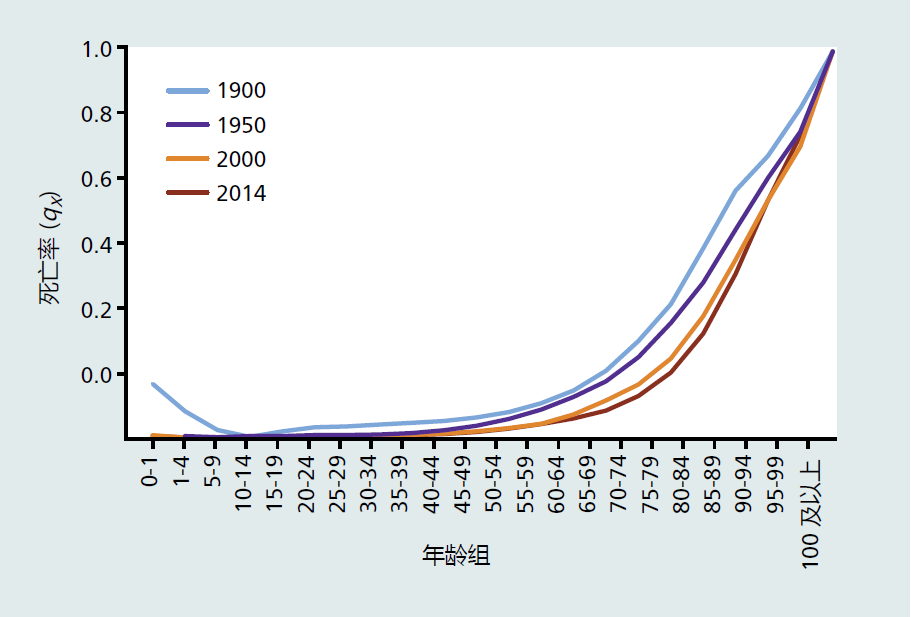
图2.11 美国总人口的特定年龄死亡率qx。这里显示的是1900年、1950年、2000年和2014年的死亡率。注意1900年至2014年间所有年龄段的死亡率(右移曲线)都在逐渐下降。(数据来自Bell FC,Miller ML 2005。United States Social Security Area 1900-2010年生命表,第11-11536号出版物。华盛顿特区:社会保障管理局;Kochanek KD等人,2016。死亡:2014年最终数据。国家生命统计报告65:1-123)。
Gompertz死亡函数,m(t)=qxeG(t) (2.3)
此处
m(t)=在t时作为年龄函数的死亡率
qx=特定年龄死亡率
e=数学常数
G(t)=t时刻的Gompertz死亡常数
此函数可以代数重写:
ln m(t)=ln qx+G(t) (2.4)
如图2.12所示,Gompertz死亡率描述了死亡率随着年龄的增长而不断增加,从而提供了发育后人口生物衰老的标志。请注意,0-1岁年龄段的死亡率不符合其他年龄组的指数增长特征。在人类群体中,从出生到1岁的个体死亡率定义了婴儿死亡率,并且由于出生和婴儿期的固有风险,将始终显著高于其他儿童期的死亡率。尽管如此,婴儿死亡率在整个二十世纪都有所下降(图2.11)。婴儿死亡率对老龄化的影响将在后面的章节中讨论。此外还要注意10-15岁和15-20岁之间的死亡率略有上升。衰老学家将这种上升称为“我认为我是不朽的”效应,因为男性倾向于从事导致死亡的危险行为。它也被称为“愚蠢或睾丸激素激增”。 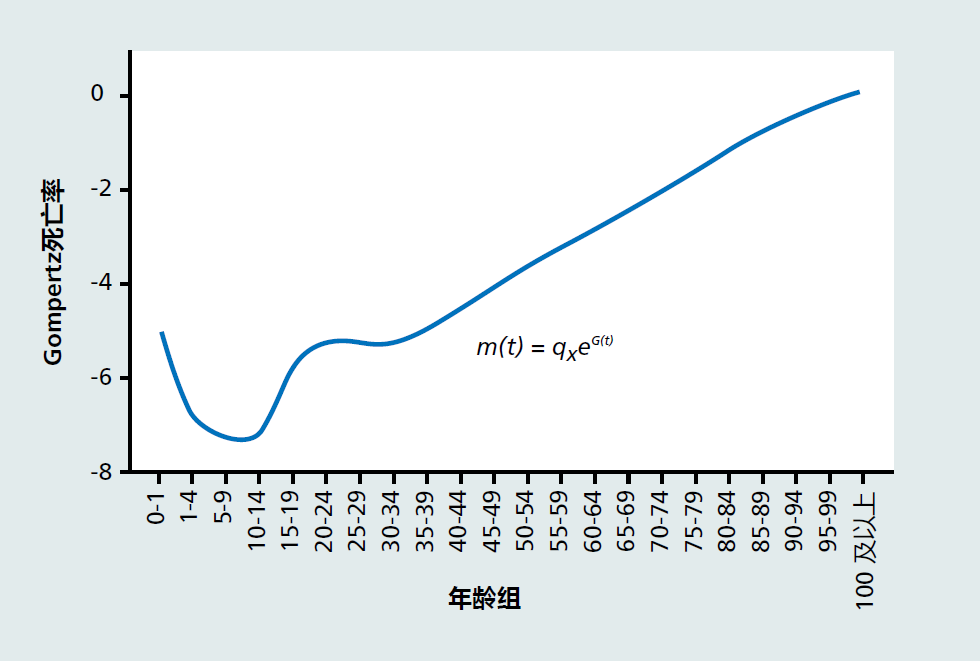
图2.12 美国总人口的Gompertz死亡率,m(t)。(数据来源于Arias E.2006.《国家生命统计报告》58:1-401010.经国家卫生统计中心许可。)
与年龄无关的死亡率会影响死亡速率
Gompertz认为,所有人口成员,即使是非常年轻的人,都是由于年龄依赖性死亡或生物老化而自然死亡的。然而,死亡可能是由事故或其他环境诱发的创伤(如感染)造成的,这些创伤并不反映生物衰老。此外,目前对年龄相关死亡率的理解在很大程度上不包括青春期前的死亡。非生物衰老导致的死亡称为与年龄无关的死亡率,可以作为一个变量包含在Gompertz死亡率函数中。一般的,只有当重大的环境影响到同一物种的不同种群死亡率时,与年龄无关的死亡率才能包含于Gompertz死亡率函数中,例如战争,传染病等等(图2.13)。此外,大多数研究表明,在青春期之前,与年龄无关的死亡率变化很大,然后在相对稳定的环境中变得恒定(图2.14)。因此,Gompertz死亡率函数(方程式2.3)的计算通常不包括青春期前的特定年龄死亡率数据。换句话说,函数的计算从死亡率最低的数据开始,通常在青春期前后。 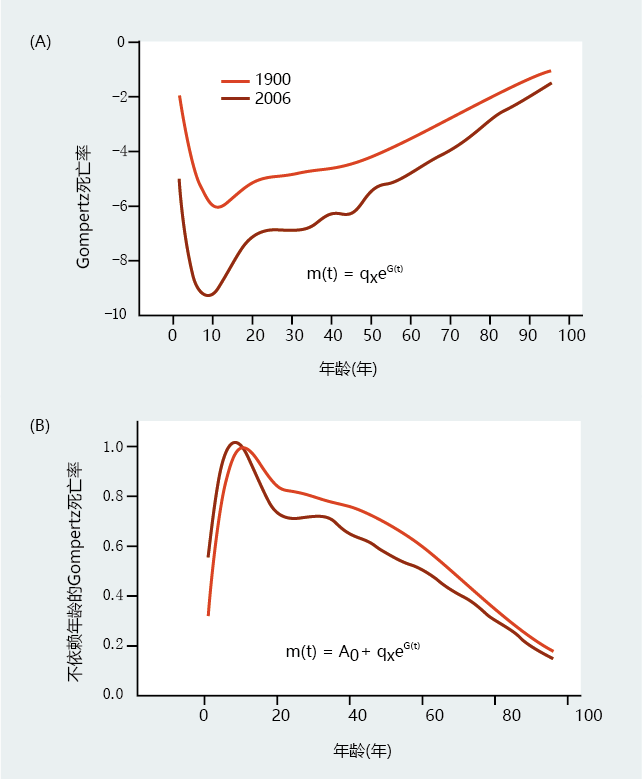
图2.13 Gompertz死亡率函数与年龄无关的Gompertz死亡率函数的比较。这些图表通过绘制(A)标准Gompertz死亡率函数和(B)具有常数A0的标准Gompertz死亡率来说明年龄无关死亡率(每个人口的最低死亡率被用作年龄无关死亡率),显示了1900年和2006年美国的死亡率。注意,(A)中所示的早期死亡率差异通过校正年龄无关死亡率来部分的消除。(数据来自贝尔FC,Miller ML.2005.美国社会保障地区1900-2010年生命表,华盛顿特区第11-11536号出版物:社会保障管理局;数据来自阿里亚斯E.2006.国家生命统计报告58:1-40,2010.经国家卫生统计中心许可。) 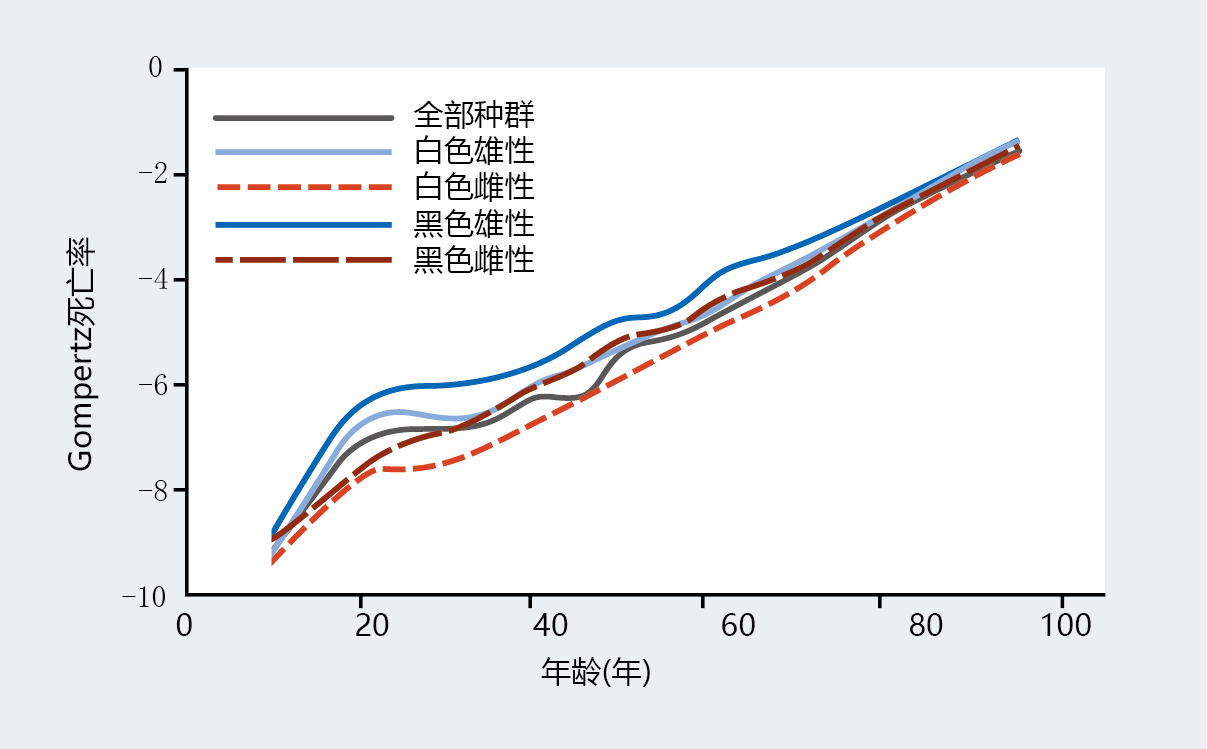
图2.14 不同美国人口的Gompertz死亡率图。所有人群的死亡率最低发生在10岁左右。虽然这四个群体的死亡率在青年期有所不同,但40岁以后的死亡率是相似的。(数据来源于Arias E.2006.《国家生命统计报告》58:1-401010.经国家卫生统计中心许可。)
由于年龄相关和年龄无关的死亡率已经被定义,并且可以用数学方法来处理,我们现在有了一种方法,在同一物种的种群之间或种群内,通过使用Gompertz死亡率函数来评估老龄化率,这些种群可能会经历不同的条件,例如社会经济状况,疾病的治疗、污染等。人口学中使用了许多统计技术来比较不同人群之间的死亡率。就本文而言,可以通过检查Gompertz死亡率函数生成的直线的斜率提供了一种确定衰老率可能变化的简单方法。例如,图2.15所示的假设Gompertz图说明了基于死亡率分析的三种不同的衰老率。A线表明人口老龄化非常迅速。B线近似于人口老龄化是渐进的Gompertz函数。平线C,斜率=0,表示似乎没有经历衰老的种群。现在考虑人口老龄化可以通过线B来描述。如果我们将一种治疗方法(例如肺癌)引入人群中,在适当的时间之后,我们可以使用Gompertz分析再次测量衰老率。如果B线向C线方向改变,那么我们可以得出结论,我们通过治疗肺癌减缓了人口老龄化的速度。如果这条线向A线移动,那么我们可以得出结论,治疗肺癌增加了衰老的速度。 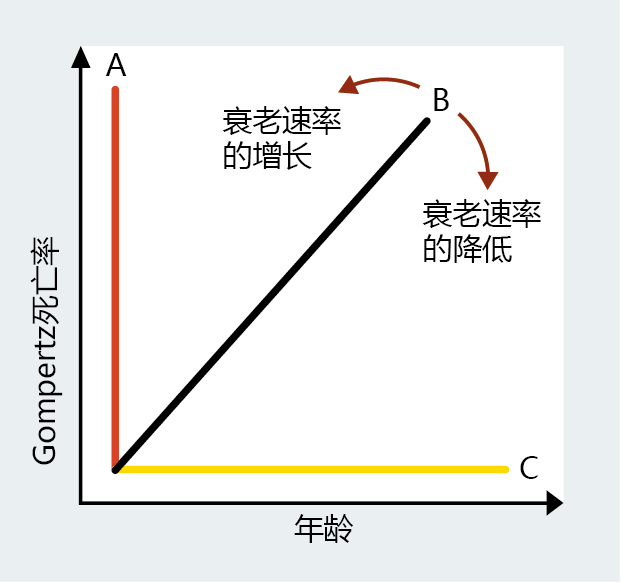
图2.15 Gompertz死亡率斜率的变化提供了人口衰老率变化的度量。随着坡度向A线移动,衰老速度增加。随着坡度向C线移动,衰老速率降低。
死亡率倍增时间校正了初始死亡率的差异
使用Gompertz分析来测量单个物种种群的衰老率已被证明对生物衰老学家非常有用。然而,不同物种的衰老率之间的比较,虽然可以通过Gompertz分析进行,但可能很难解释,因为种群规模、与年龄无关的死亡率和最大寿命在物种之间存在很大差异(图2.16)。虽然一些人口学家已经开发出复杂的数学方案来解释这些差异,但这些程序包括许多不容易应用于所有物种的假设和技术。Calab Finch在1990年提出,通过简单计算死亡率倍增时间(MRDT)或种群死亡率倍增所需的时间,可以部分减少使用Gompertz分析进行物种间的比较所带来的困难,如下公式2.5:
死亡率倍增时间MRDT=ln2/G=0.693/G (2.5)
此处
ln2=2的自然对数
G=Gompertz死亡率常数
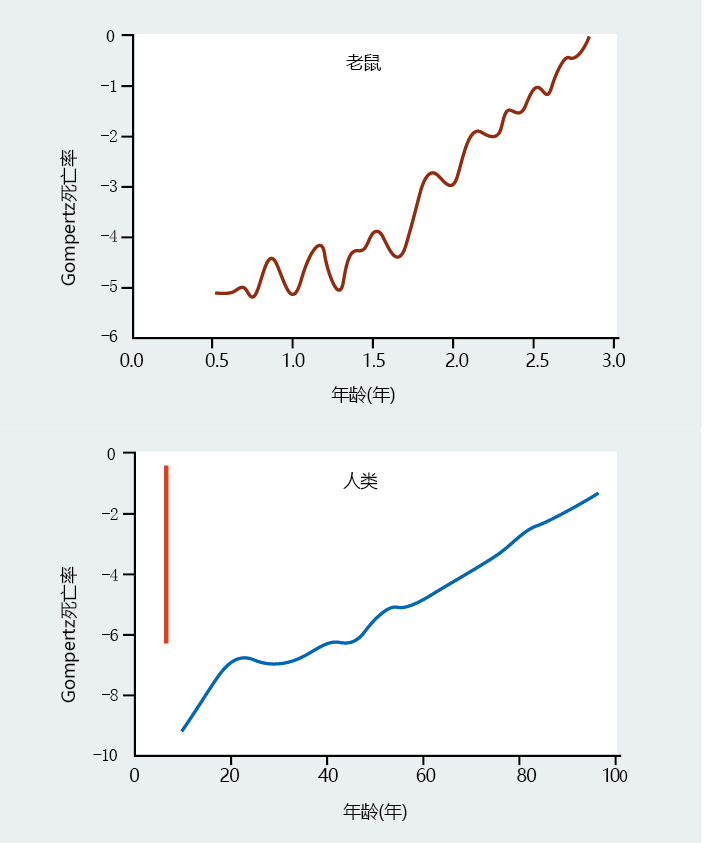
图2.16 两种不同物种的Gompertz死亡率比较。这些图表显示了2006年小鼠种群和美国总种群的Gompertz死亡率图。尽管小鼠数量少会导致数据发生显著变化,但请注意,特定年龄(小鼠为1.5岁,人类为25-30岁)后的死亡率模式相似,并且描述了一种逐渐衰老的速度。然而,与年龄无关的死亡率和最大寿命的差异可能很难在物种之间进行比较。如果我们将小鼠数据绘制在与人类数据相同的x轴刻度上,结果将是人类绘图上的红线。(底部数据来自Arias E.2006.Natl Vital Stat Rep 58:1–402010.经国家卫生统计中心批准。)
包括MRDT在内的衰老速率分析通常是检验个体衰老速率假设的基础。例如,考虑表2.3中的人、狗和蝙蝠的数据。初始死亡率(IMR)告诉我们,人类已经非常擅长在生命早期限制死亡率。较高的IMR表明,因为蝙蝠是野生动物,在保护幼崽方面不如人类。此外,蝙蝠的最大寿命只有人类的20%左右。如果我们只用这两个变量作为人口衰老速率的标志,一个合乎逻辑的结论是,IMR显著影响最大寿命。然而,请注意,家养狗的IMR介于人类和蝙蝠之间,但最大寿命等于蝙蝠的寿命。因此,IMR不太可能决定寿命。我们必须找到另一个答案来解释为什么不同物种的最大寿命不同。将MRDT添加到分析中,可以对可能发生的情况提供一些见解。
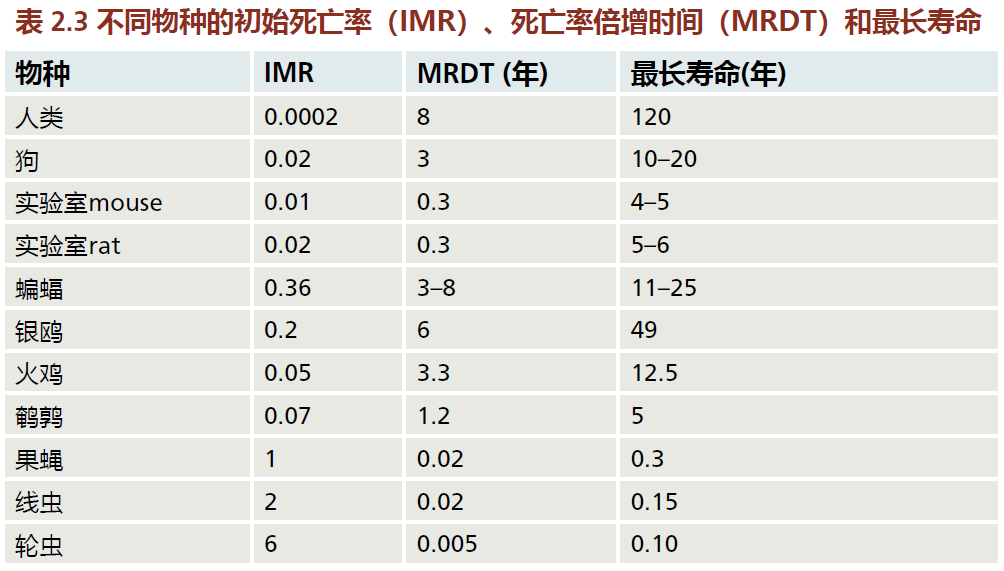
虽然蝙蝠的IMR很高,但它们的平均MRDT为5年,这表明它们的衰老速度比驯养狗的MRDT为3年的衰老速度要慢。然而,我们必须考虑,驯养的狗通常能得到人类所获得的几项医疗福利。这很可能通过降低与年龄无关的死亡率来延长狗的寿命。蝙蝠是野生的,因此由于捕食和疾病,繁殖后的寿命往往很短。换句话说,与狗相比,蝙蝠的死亡率与年龄无关。尽管如此,5年的MRDT表明蝙蝠的衰老速度比狗更接近人类。蝙蝠的MRDT也明显高于在老鼠和大鼠身上观察到的MRDT,老鼠和大鼠是衰老研究中最常见的两种物种。考虑到有助于降低与年龄无关的死亡率的适当环境条件,蝙蝠将成为人类评估影响个体衰老率的可能因素的良好模型。事实上,许多实验室正是为了这个目的而圈养繁殖蝙蝠。
生存曲线近似于死亡率
生命表的构建和死亡率的分析非常耗时,而且通常很复杂。此外,准确确定死亡率需要大量的群体样本,这是大多数生物学家所没有的奢侈品。因此,生物衰老学家使用更简单的生存曲线(一种随时间变化的生存率图形表示)来估计人口中的衰老速率(图2.17)。适用于寿命表的关于衰老速率的一般假设也可用于生存曲线。事实上,将存活曲线的形状与死亡率的对数进行比较表明,随着死亡率性质的变化,存活曲线的形状也会发生变化(图2.18)。
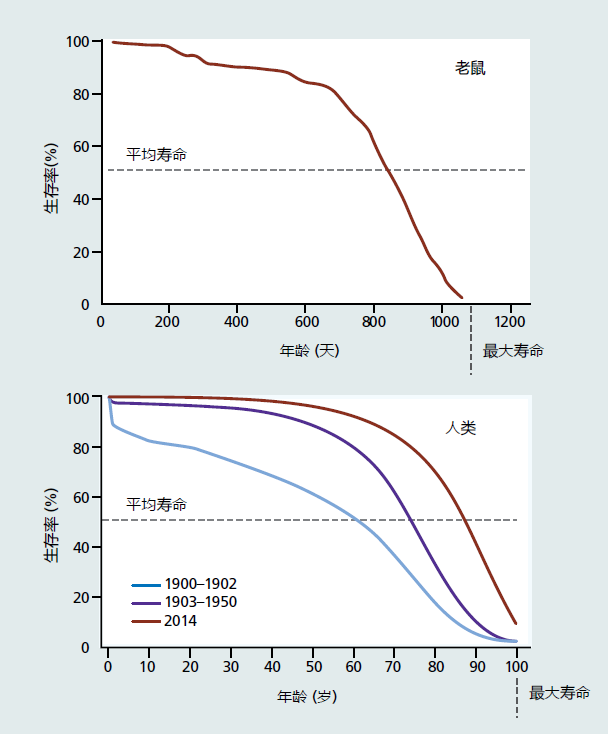
图2.17 两种不同物种的存活曲线比较。生存曲线由生命表生成(见表2.2)。第1列(年龄)与第3列(lx)与寿命百分比的转换相对应。2006年小鼠种群和人类种群的存活模式相似,这表明小种群的存活曲线很好地接近真实死亡率。(底部数据来自Arias E.2006.Natl Vital Stat Rep 58:1–402010.经国家卫生统计中心批准。)
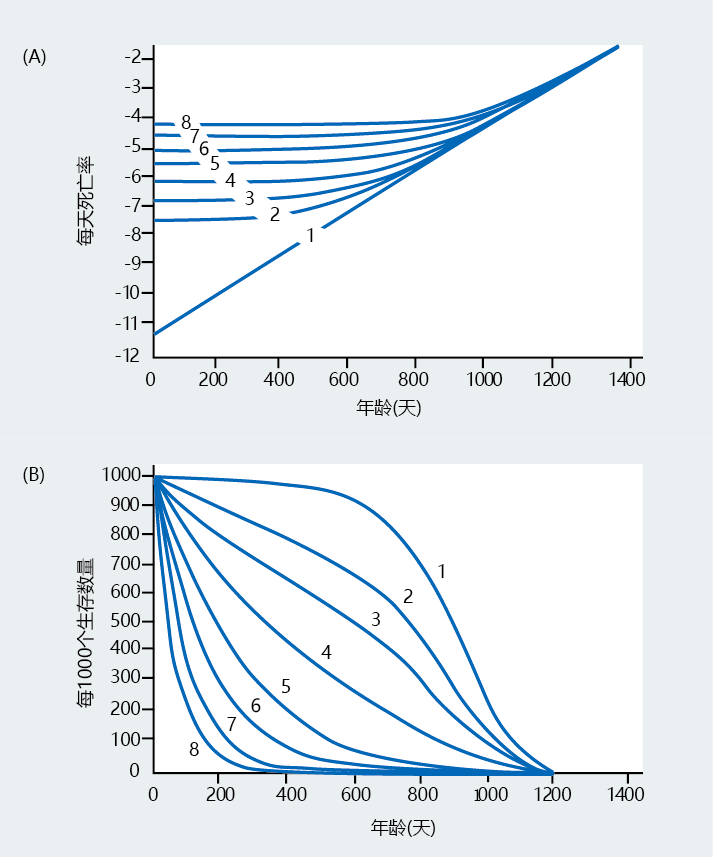
图2.18 Gompertz死亡率曲线和存活曲线的比较。(A) Gompertz图像。(B) 生存曲线。线条上的数字表示两张图中的同一个种群。例如,(A)中的第1行,即逐渐老龄化的人群的预期死亡率,对应于(B)中的第1行,即相同人群的预期生存曲线。随着Gompertz死亡率模式的改变,生存模式也随之改变,这表明生存曲线是死亡率的一个很好的近似值。(摘自佐治亚州Sacher 1977年出版的《衰老生物学手册》[CE Finch,L Hayflick,eds.],纽约:Van Nostrand Reinhold。经John Wiley and Sons公司许可。)
用于构建生存曲线的数据还提供了两个重要变量:平均寿命和最大寿命,这两个变量在生物衰老学中广泛使用。平均寿命相当于人群寿命的算术平均值。最大寿命反映了人群中寿命最长个体的死亡年龄。生物衰老学家通常使用存活率的10%作为他们最大寿命的标志,因为存活曲线通常是由数量较少的人群生成的,很少有人达到非常高龄。就影响生存曲线形状的因素而言,平均寿命和最大寿命都有特定的含义。
平均寿命是衡量人口外在衰老的一个指标。生物衰老学家比较了暴露于不同环境或实验处理的单一物种种群的平均寿命,以确定外部因素是否影响种群衰老的速度。请注意,图2.17中所述的前50%人口的死亡需要经历一个较长的时间。第二个50%的人口在生命周期的短时间内死亡。因此,平均寿命是发育和成熟阶段存活率以及这两个生命阶段对衰老的影响的相对度量。注意图2.17所示的人类早期生存率的变化如何改变平均寿命。平均寿命的积极变化表明,一些外部干预减缓了衰老的外在速度,并允许更大比例的人口进入衰老。相反,平均寿命的负变化意味着外在衰老率的增加和衰老个体的减少。达到衰老的个体越少,那么关于最大寿命受到选择性死亡率的影响这种结论的可能性就越大。
最大寿命为生物衰老学家提供了一些关于遗传或内在衰老速率的信息。在接下来的章节中,你将了解到,寿命潜能是从基因进化而来的,尽管这些基因尚未被识别。因此,在某些治疗或实验程序后,最大寿命的任何变化都可能意味着内在衰老的一些基本特性已经发生了改变(很可能是遗传性的)。请注意,图2.17中三个人群的最大寿命是相同的,尽管存活曲线的形状不同。也就是说,最大寿命不受外在衰老速率的影响。
生物衰老时死亡率的降低表明了长寿基因的可能性
仔细观察图2.17中的存活曲线表明,在这些人群的寿命接近尾声时,存活率略有增加。存活曲线尾部的死亡率变化是一个常见的观察结果,表明晚年死亡率可能会降低,而不是像Gompertz预测的那样保持不变。一些研究人员已经调查了这种可能性,并发现在晚年,当研究人群在生命结束时有足够的个体数量来进行精确分析时,死亡率会下降。第一个认识到这一现象的是加利福尼亚大学戴维斯分校的James Carey。他用120多万只地中海果蝇来证明果蝇的死亡率在老年时会下降(图2.19)。这些发现的含义是,Gompertz死亡率函数不能准确地描述生命各个阶段的死亡率轨迹,也无法准确地预测人口的最大寿命。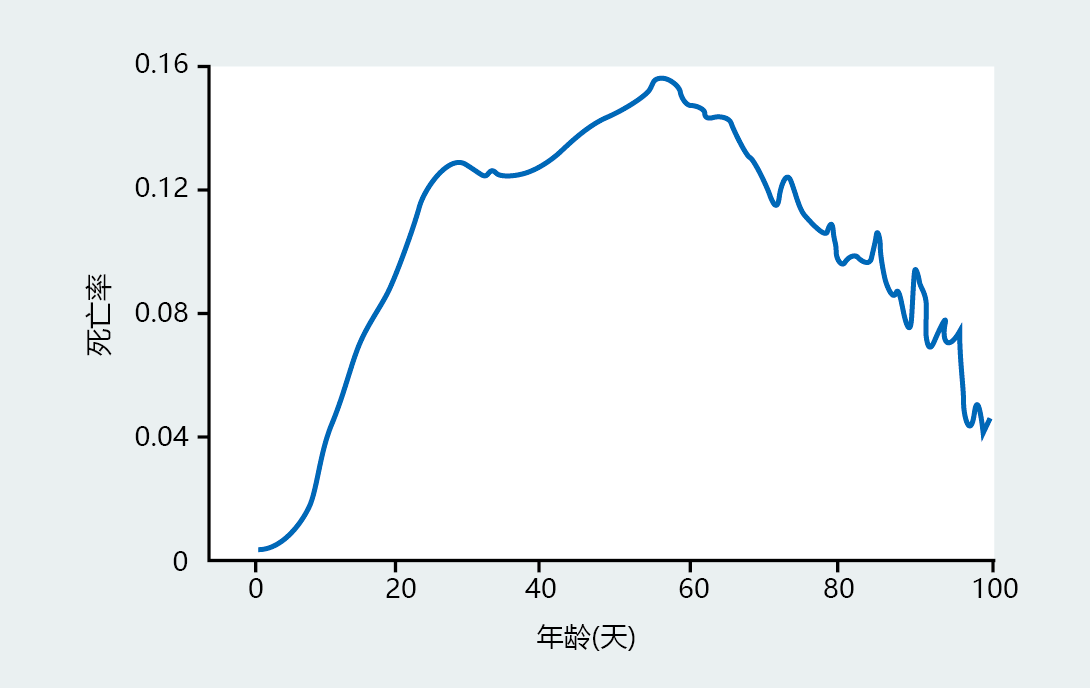
图2.19 120万只果蝇的死亡率。从0日龄到20-30日龄,该比率显示了在实验室条件下的种群预期的典型指数增长,即与年龄无关的死亡率很低。然而,对这一庞大果蝇种群的分析表明,与Gompertz预测的恒定死亡率不同,果蝇的死亡率在晚年会减慢。(摘自Carey JR等人,1995年,Exp Gerontol 30:605–629,经Elsevier许可。)
既然在任何已知衰老的物种中都没有观察到永生,那么最大寿命可能不固定的发现有实际应用吗?很可能不是。但是,晚年死亡率的降低对研究衰老进化和遗传学的生物衰老学研究者有着巨大的理论意义。正如你在下一章所了解到的,进化论预测长寿是由基因决定的;也就是说,基因决定寿命。果蝇的数据与进化理论相一致,表明果蝇种群的这个亚群与大多数种群具有不同的寿命特征。由于寿命是由基因组决定的,因此,果蝇的这一亚群必须具有不同的基因,使它们能够以不同的速度长寿和衰老。因为对果蝇的研究提供了理论基础,因此分子生物学家和遗传学家正在使用这些理论来寻找这些可能改变寿命的基因。
精确医学时代将改变我们测量人口衰老速率的方式
您了解到,测量死亡率可以深入了解人口老龄化的速度。然而,死亡率仅为单一时间点(死亡)的衰老速率提供一个标志。我们已经看到死亡和衰老是不一样的(见第一章)。此外,死亡率并没有提供任何关于可能导致活着的种群衰老速率的信息。老年学家除了使用死亡率外,还使用残疾率或功能丧失率来更好地理解人口老龄化。
依赖于时间的功能丧失为老年学家提供了一个标志,表明人口在整个生命周期中都在老龄化,而不仅仅是在生命结束时才开始。时间依赖性功能丧失作为人口衰老速率的标志,传统上是通过发病率、人口疾病数量来评估的。人口发病率代表了普通人感染疾病的统计概率。(发病率的主要衡量标准:发病率、患病率和风险在第9章中讨论。)发病率作为人口老龄化的替代指标一直被认为是有效的,直到20世纪60年代末和70年代初,因为美国和大多数经济发达国家的主要死因被认为是急性疾病,诊断后存活率较低。变老通常意味着疾病在生殖后的早期发展,并且导致功能丧失和死亡。然而,如今,预防、诊断和治疗方面的进步已经将包括心脏病和癌症在内的许多疾病转变为慢性病。在诊断出一种曾经致命的疾病后,获得相对正常的寿命已变得司空见惯。因此,即使个人可能患有疾病,衰老的过程仍在继续。我们曾经问过这样一个问题:“衰老如何影响疾病?”我们现在可以问,“疾病是如何影响衰老的?”
通过测量人口中的发病率,人口统计学家可以为普通人的衰老速率提供一个定义明确、独立且稳定的指标。正如你在上一节中所了解到的,精确医学时代将为疾病带来一种新的分类,这种分类将是动态的,包括个体独特基因组和环境相互作用的高度个性化。“普通人”对患疾病的风险几乎没有意义,对确定人口衰老速率的价值更是微乎其微。这意味着,老年人口学家还必须是信息共享社区的成员,并需要开发新的人口衰老速率统计模型,以解释个人的基因组、行为和环境状况。这些统计模型是什么样子,现在谁也猜不透。


