3.2 进化与长寿
外在的衰老速度会导致自然选择力的下降
Weismann和Fisher关于长寿的假设的第一个正式应用来自Peter Medawar爵士(1915-1987)。Medawar使用了年龄结构分析的简化版本,以确定所有物质(无机物和有机物)的寿命都是由外部因素造成的。此外,外在衰老速率(由于环境危害导致的种群衰老速率)让许多人认为长寿进化基础的如下基本原则:自然选择的能力随着年龄的增长而下降。
1951年,Medawar提出了一个实验来证明这一原理。想象一下,一个拥有1000个试管“群体”的初创实验室。尽管试管不会老化,但每个月都有正好10%的试管在外部环境因素的随机事故中破裂。实验室的工作人员更换破损的管子,以便每个月初的总数始终为1000。也就是说,试管的总数量处于平衡状态。幸运的是,对于我们的演示,实验室主任要求所有试管都标明它们进入实验室的日期。因此,我们可以追踪1000个原始个体的生活史,如图3.7所示。
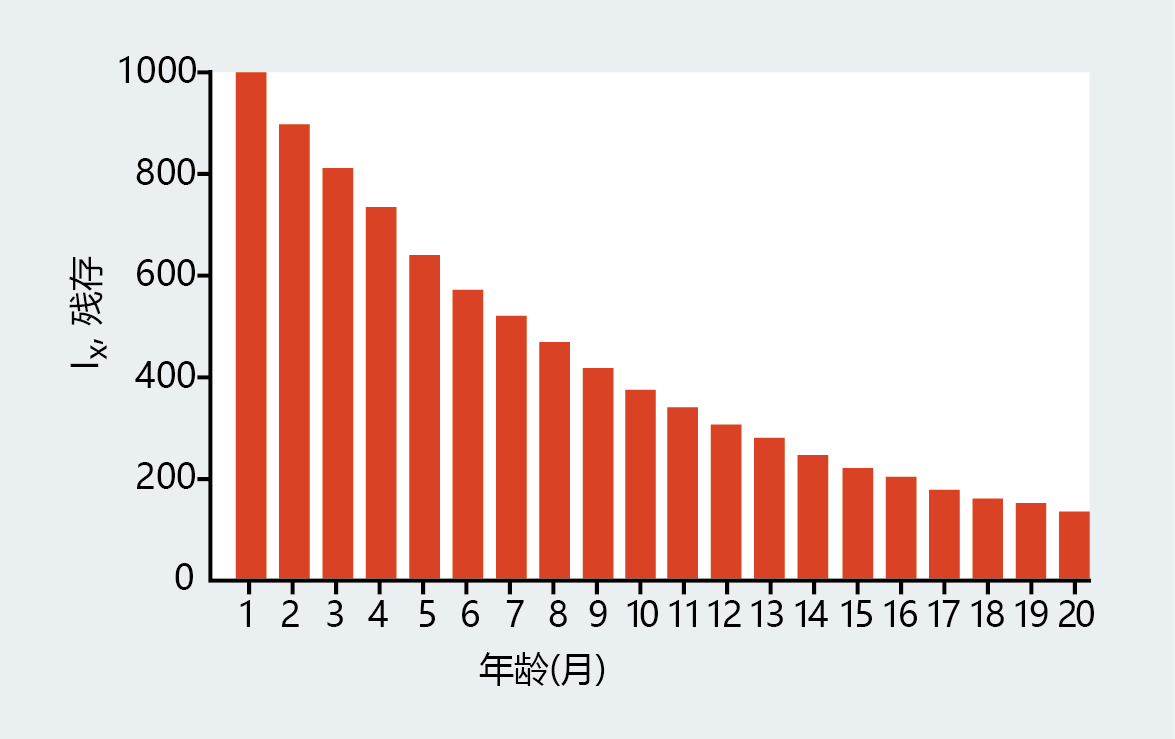
图3.7 Medawar实验中试管“群体”的生活史。该图显示了1000个原始群体中存活的试管数量(存活率,lx),假设每月10%的固定死亡概率。(改编自Medawar PB,1952年。一个尚未解决的生物学问题。伦敦:H.K.Lewis and Company。)
图3.7所示的年龄结构分布描述了一个群体,其中任何年龄组的幸存者数量总是超过后续年龄组的幸存者数量。在这一群体中,一组试管的存活率高于下一组试管的存活率不能归因于脆弱性的增加,因为没有衰老,也就是说,没有增加死亡概率的内在因素。死亡之所以发生,仅仅是因为随着年龄的增长,试管暴露在外部环境危害下的时间更长,因此破裂的风险增加。通过对一个非遗传的、寿命极长的人群的描述,Medawar建立了外在的老龄化率。在第四章中,你会看到,随着时间的流逝,人们越来越多地暴露在外部环境的危害中,这是与衰老相关的生理衰退的基础。
现在考虑参数的微小变化。我们没有让实验室人员更换试管,而是假设图3.7中描述的群体中的每个年龄组都奇迹般地获得了繁殖能力。幸运的是,它们以每月10%的恒定速度繁殖(图3.8)。输卵管仍然不会老化,所有个体,无论年龄多大,都具有相同的生育能力。然而,这并不意味着每个年龄组都将为总的群体的更新做出同等贡献。显然,1-2个月年龄组(900个中的10%)的试管数量远大于13-14个月年龄组(273个中的10%)。因此,年轻群体对种群更替的贡献更大,不是因为它们更有男子气概,而是因为它们没有像老年群体那样长期暴露在环境危害之下。在本演示的下一步中,试管不再本质上对衰老免疫。到了一定年龄,它们会变得虚弱,失去自我繁殖的能力。生殖开始衰退的年龄对我们试管种群的生存有影响吗?确实如此。想象一下,生殖能力的丧失发生在生命的早期,比如2-3个月大的时候。这将对物种的延续造成灾难性的后果,试管很快就会从我们的实验室消失。然而,如果衰老和繁殖丧失发生在15-16个月,结果将明显减少后代总数,但不会对物种的延续产生重大影响。换句话说,年龄较大的群体是否对试管的基因库有贡献变得无关紧要。当适应度接近于零时,自然选择的力量就会减弱。

图3.8 Medawar试管“群体”的后代数量和年龄之间的关系。假设试管以每月10%的恒定速率繁殖,并且死亡概率保持在10%不变,那么较年轻的群体将比较年长的群体产生更多的后代,因为较年轻的试管比年长的试管多。Medawar的这一简单观察描述了自然选择力随年龄下降的原因。(改编自Medawar PB,1952年。一个尚未解决的生物学问题。伦敦:Lewis and Company。)
Medawar认为衰老是遗传漂变(genetic drift)的结果
Medawar对生物体内衰老和/或长寿的进化过程的解释与Weismann的解释有着同样的悖论。也就是说,如果自然选择的力量随着年龄的增长而减弱,而衰老发生在生殖开始之后,那么与衰老相关的生理衰退是如何成为生物体基因组成的一部分的呢?回想一下,Weismann解决了这个悖论,他认为衰老与生殖无关。因为Weismann的思想是在孟德尔的遗传原理被了解之前发展起来的,所以他无法用经典遗传学来解释他的推理。另一方面,Medawar生活在一个遗传原则已经牢固确立的时代,大多数科学家相信基因决定论,即只有通过自然选择和特定生物过程才能选择基因的过程。(我们现在知道还有其他基因选择机制,一个基因可以参与几个相关但独立的过程。)因此,Medawar需要一种理论来解释衰老是如何发生的,在没有自然选择的情况下,衰老是一个与生存和繁殖相反的过程,并受到基因的调控。他对衰老现象的解释是基于遗传漂变原理的,在这个过程中,由于减数分裂时等位基因的随机排序,基因可以固定在一个小群体中。Medawar关于衰老进化的理论被称为衰老的突变积累理论。
让我们看一个例子。假设一个较小的老年群体有两个编码生殖后寿命的等位基因:一个显性等位基因导致较短的生殖后寿命(SL),另一个隐性等位基因导致较长的生殖后寿命(ll)。如图3.9所示,这个小型衰老群体在遗传上分为经典的孟德尔分布:四分之一隐性和四分之三显性(1/4 llll、1/2 SLll、1/4 SLSL)。由于老年个体的高外在衰老率和低适应性,只有两对(四个个体)能够繁殖。这些交配对纯属偶然。在导致ll等位基因固定的路径中(图3.9中的左路径),一对交配的两个个体都含有隐性等位基因的两个副本;另一对的两个个体都含有ll和SL等位基因的一个拷贝。对于完全隐性交配对(llll),唯一可能的后代也是完全隐性的。通过在减数分裂时对等位基因进行随机排序,具有混合等位基因的配对也可能产生完全隐性的后代。因此,隐性ll等位基因成为显性基因LLLL纯属偶然,但却是一种真正的可能性。可以证明消除ll等位基因的类似统计策略(如图3.9中的右边路径所示)。
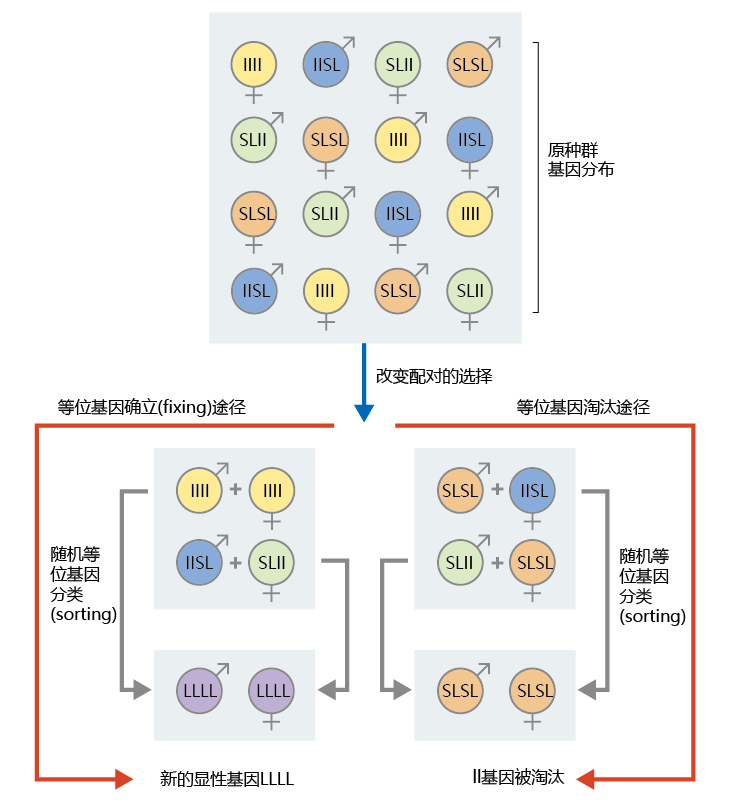
图3.9 遗传漂变和突变累积导致的基因固定。在这个群体中,SL是导致生殖后寿命较短的显性等位基因,ll是导致生殖后寿命较长的隐性等位基因。左边的路径说明了等位基因的偶然交配和随机排序如何导致隐性ll等位基因成为显性基因LLLL。正确的路径说明了如何从群体中消除隐性ll等位基因。
Medawar提出,在生殖后群体中,衰老和长寿是分开出现的
回想一下,Medawar生活在一个基因决定论被完全接受的时代。如果观察到一个生物事件(衰老被视为一个生物事件),那么就有一个基因在调节这个过程。因此,Medawar需要从遗传学角度解释衰老是如何被调控的,衰老是生殖后功能的缓慢下降。他推断,单一基因不会导致衰老,因为具有巨大有害影响的单一基因最终会从基因组中消除。相反,衰老更密切地反映了数百个甚至数千个基因的适应,这些基因具有小的、非致命的、但具有负面的影响。Medawar关于衰老进化基础的思想源于亨廷顿氏病(Huntington's chorea)的例子。亨廷顿氏病是一种神经系统疾病,由一种隐性突变引起,这种突变在中年(30岁晚期至40岁中期)表达,并且总是致命的。因此,如果只有一个基因导致衰老,携带亨廷顿氏病基因的人在基因漂变将该基因固定在基因组中之前,就已经将这个基因从人群中消除了。但非致命、有害的基因可能会变得固定(1)因为参与基因传递的群体很小,所以抵抗这些基因的选择压力会很低,(2)因为基因漂变。
Medawar的文章没有明确说明他是否理解导致分子结构破坏的外在因素可能导致有机生命的衰老。最有可能的是,为了与他那个时代的科学保持一致,Medawar会认为有机物不会受到导致非有机物衰老的物理力的影响。我们现在知道,热力学力,包括熵,也适用于有机物(见第4章)。然而,Medawar为衰老是一个随机过程的理论奠定了基础,该过程是由热力学力产生的,而寿命是通过自然选择进化而来的,是对生存到生殖年龄至关重要的基因的副产品。
Hamilton的自然选择对死亡率的影响完善了Medawar的理论
突变积累的基础在于观察到繁殖力和死亡率之间存在权衡;最高的繁殖力,也就是适宜性,发生在死亡率最低的时候。在提出突变累积的可能性时,Medawar依赖于Fisher参数r及其导数生殖值vx作为适应度的度量。然而,Medawar并没有用数学上明确的术语解释他的理论,但这是理论进化生物学的关键一步。W·D·Hamilton(1936-2000)来完成下一步,采取科学解释长寿进化理论。
Hamilton认识到,在整个生命周期中整合生殖潜力是衡量适应度是一种不精确的方法。他假设,任何种群,即使是稳定的种群,在不同的年龄段,其规模都可能发生波动,这取决于特定年龄段的死亡率。Fisher的生殖值表明,适应度更可能反映特定年龄段的生殖潜力,而不是整个生命周期的总综合价值。
为了量化自然选择的力量,Hamilton推导出了与特定年龄死亡率相关的适应度变化表达式。与Fisher的生殖值vx一样,Hamilton的自然选择对死亡率sx的影响在生殖开始后下降(图3.10A)。然而,与vx不同,sx在繁殖前是稳定的和最高的。由于外在因素使自然选择对生殖前死亡率的影响最大,进化会选择生存到生殖年龄所必需的基因。Hamilton评估衰老和寿命的方法与之前的研究一致,表明对于调节衰老或寿命的基因来说,选择压力将极其微弱。因此,如果存在长寿和/或衰老的基因,它们必须与选择存活到生殖年龄的基因相关。
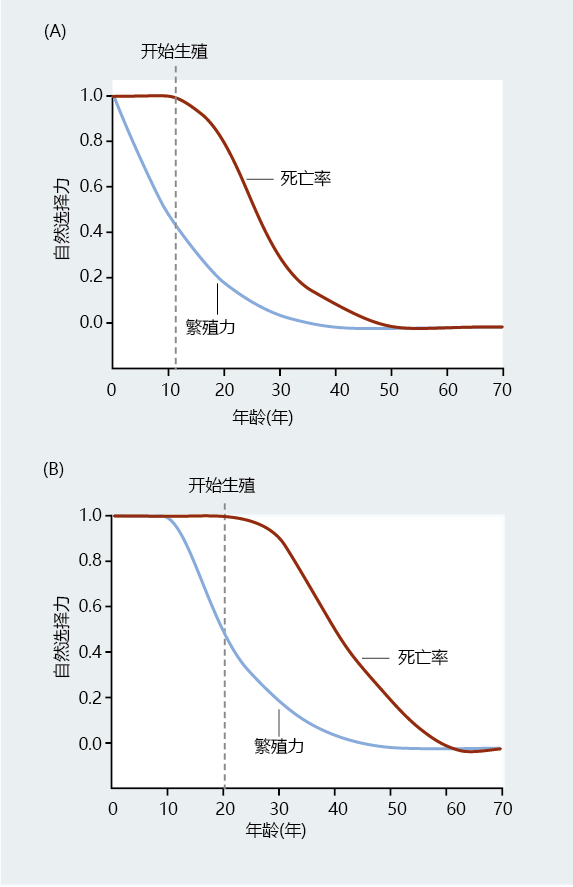
图3.10 Hamilton自然选择对死亡率和繁殖力的影响。(A) 自然选择对死亡率的影响sx作用于一个假设的人类种群。请注意,死亡率(棕色线)在生殖开始前最高(用虚线表示)。(B)同一种群中的一小部分人有晚年繁殖的基因编码。由于这一亚群中的繁殖开始的时间比在总种群中观察到的晚,自然选择对死亡率的影响被延迟。(改编自Hamilton WD.1966.J Theoret Biol 12:12–45.经Elsevier许可。)
Hamilton关于长寿的数学理论是理解长寿(而不是衰老)是如何进化的一个重大突破。例如,想象一下,一个小群体中的一些个体有编码晚年生殖的基因(图3.10B)。自然选择对死亡率的影响将在生命周期的后期开始。从理论上讲,如果没有繁殖,就不可能在繁殖力和死亡率之间进行权衡。在整个生殖过程中,对于任何给定的年龄,这一小群体在老年时都会有更大的繁殖力。
随着进化时间的推移,由于基因漂变,赋予长寿命的基因可能会固定在基因组中。Hamilton提供的数学理论表明,长寿可能是进化而来的。


